03 | 复杂度分析（上）：如何分析、统计算法的执行效率和消耗资源？

发表于 更新于 分类于 阅读次数：
我们都知道，数据结构和算法解决的是“快”和“省”的问题，即如何让代码运行的更快，如何让代码更省存储空间。所以，执行效率是算法的一个非常重要的考量指标。那如何来衡量编写的算法代码的执行效率呢？这里就要用到时间、空间复杂度分析。

为什么需要复杂度分析呢？

你可能会有些疑惑，把代码跑一遍，通过统计、监控就能得到算法执行的时间和占用的内存大小。为什么还要做时间、空间复杂度分析呢？

首先，这种评估算法执行效率的方法是正确的。很多数据结构和算法书籍还给这种方法起了个名字，叫事后统计法。但是，这种统计方法有非常大的局限性。

  1. 测试结果非常依赖测试环境
  2. 测试结果受数据规模的影响很大

所以就需要一个不用具体的测试数据，就可以粗略的估计算法执行效率的方法。这就是时间、空间复杂度分析方法。

大O复杂度表示法

算法的执行效率，粗略地讲，就是算法代码的执行时间。

直接上代码，求1,2,3…n的累加和。估算一下这段代码的执行时间。

1
2
3
4
5
6
7
8
int cal(int n){
	int sum = 0;
	int i = 1;
	for (; i<=n; i++){
		sum = sum + i;
	}
	return sum;
}

从CPU的角度来看，这段代码的每一行都执行着类似的操作：读数据-运算-写数据。尽管每行代码对应的CPU执行的个数、时间都不一样，但是，我们这里只是粗略的估计，所以可以假设每行代码执行的时间都一样，为unit_time(以下简称为ut)。在这个假设的基础上，这段代码的总执行时间是多少呢？

第2、3行代码分别需要1个$ut$的执行时间，第4、5行都运行了$n$遍，所以需要$2n*ut$的执行时间，所以这段代码总的执行时间就是$(2n+2)*ut$。可以看出来，所有代码的执行时间$T(n)$与每行代码的执行次数成正比。

按照这个分析思路，再来看这段代码。

1
2
3
4
5
6
7
8
9
10
11
12
int cal(int n){
	int sum = 0;
	int i = 1;
	int j = 1;
	for (; i<=n; i++){
		j = 1;
		for(; j<=n; j++){
			sum = sum + i * j;
		}
	}
	return sum;
}

依旧假设每个语句的执行时间是$ut$。那这段代码的总执行时间$T(n)$是多少呢？

第 2、3、4 行代码，每行都需要1个$ut$的执行时间，第 5、6 行代码循环执行了$n$遍，需要 $2n*ut$的执行时间，第 7、8 行代码循环执行了$n^2$遍，所以需要 $2n^2 * ut$ 的执行时间。所以，整段代码总的执行时间$T(n) = (2n^2+2n+3)*ut$。

尽管我们不知道$ut$的具体值，但是通过这两段代码执行时间的推导过程，我们可以得到一个非常重要的规律，那就是，所有代码的执行时间$T(n)$与每行代码的执行次数$n$成正比。

我们可以把这个规律总结成一个公式。注意，大$O$就要登场了！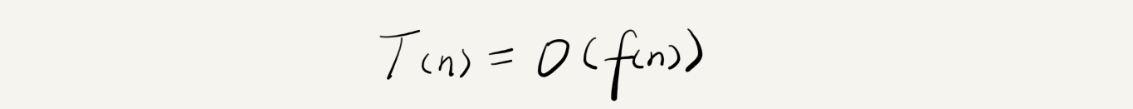
01

其中，$T(n)$表示代码执行的时间; $n$表示数据规模的大小; $f(n)$表示每行代码执行的次数总和,因为这是一个公式，所以用$f(n)$来表示。公式中的 $O$，表示代码的执行时间$T(n)$与$f(n)$表达式成正比。

所以，第一个例子中的$T(n) = O(2n+2)$，第二个例子中的$T(n) = O(2n^2+2n+3)$。这就是大$O$时间复杂度表示法。大$O$时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，也叫作渐进时间复杂度，简称时间复杂度。

当$n$很大时，可以把它想象成10000、100000。而公式中的低阶、常量、系数三部分并不左右增长趋势，所以都可以忽略。只需要记录一个最大量级就可以了，如果用大$O$表示法表示刚讲的那两段代码的时间复杂度，就可以记为：$T(n) = O(n)$； $T(n) = O(n^2)$。

时间复杂度分析

1. 只关注循环执行次数最多的一段代码

大$O$复杂度表示法只是表示一种变化趋势。通常会忽略掉公式中的常量、低阶、系数，只需要记录一个最大阶的量级就可以了。所以，在分析一个算法、一段代码的时间复杂度的时候，只关注循环执行次数最多的那一段代码就可以了。

1
2
3
4
5
6
7
8
int cal(int n) {
	int sum = 0;
	int i = 1;
	for (; i <= n; ++i) {
		sum = sum + i;
	}
	return sum;
 }

其中，第2、3行代码都是常量级的执行时间，与$n$的大小无关，所以对于复杂度并没有影响。循环执行次数最多的是第4、5行代码，所以这块代码要重点分析。这两行代码被执行了$n$次，所以总的时间复杂度就是$O(n)$。

2. 加法法则，总复杂度=量级最大的那段代码的复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int cal(int n) {
	int sum_1 = 0;
	int p = 1;
	for (; p < 100; ++p) {
		sum_1 = sum_1 + p;
	}

	int sum_2 = 0;
	int q = 1;
	for (; q < n; ++q) {
		sum_2 = sum_2 + q;
	}
 
	int sum_3 = 0;
	int i = 1;
	int j = 1;
	for (; i <= n; ++i) {
		j = 1; 
		for (; j <= n; ++j) {
			sum_3 = sum_3 +  i * j;
		}
	}
 
	return sum_1 + sum_2 + sum_3;
}

第一段代码循环执行了100次，所以时间复杂度是一个常量，与$n$的规模无关。

这里要再强调一下，即便这段代码循环10000次、100000次，只要是一个已知的数，跟$n$无关，照样也是常量级的执行时间。当$n$无限大的时候，就可以忽略。尽管对代码的执行时间会有很大影响，但是回到时间复杂度的概念来说，它表示的是一个算法执行效率与数据规模增长的变化趋势，所以不管常量的执行时间多大，我们都可以忽略掉。因为它本身对增长趋势并没有影响。

第二段和第三段代码的时间复杂度分别是$O(n)$和$O(n^2)$。

综合这三段代码的时间复杂度，我们取其中最大的量级。所以，整段代码的时间复杂度就为$O(n^2)$。也就是说：总的时间复杂度就等于量级最大的那段代码的时间复杂度。将这个规律抽象成公式就是：
如果$T1(n)=O(f(n))$，$T2(n)=O(g(n))$
那么 $T(n)=T1(n)+T2(n)=max(O(f(n))$,$O(g(n))) =O(max(f(n), g(n)))$

3. 乘法法则：嵌套代码的复杂度=嵌套内外代码复杂度的乘积

公式：
如果$T1(n)=O(f(n))$，$T2(n)=O(g(n))$
那么$T(n)=T1(n)*T2(n)=O(f(n))*O(g(n))=O(f(n)*g(n))$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int cal(int n) {
	int ret = 0; 
	int i = 1;
	for (; i < n; ++i) {
		ret = ret + f(i);
	} 
} 
 
int f(int n) {
	int sum = 0;
	int i = 1;
	for (; i < n; ++i) {
		sum = sum + i;
	} 
	return sum;
}

单看cal()这个函数，假设f()只是一个普通的操作，那第 4～6 行的时间复杂度就是：$T1(n) = O(n)$。但f() 函数本身不是一个简单的操作，它的时间复杂度是$T2(n) = O(n)$，所以，整个 cal() 函数的时间复杂度就是：$T(n) = T1(n) * T2(n) = O(n*n) = O(n^2)$。

几种常见时间复杂度实例分析

虽然代码千差万别，但是常见的复杂度量级并不多。
复杂度量级（按数量级递增）：常量阶$O(1)$、对数阶$O(logn)$、线性阶$O(n)$、线性对数阶$O(nlogn)$、平方阶$O(n^2)$、立方阶$O(n^3)$、…、k次方阶$O(n^k)$

还有两种非多项式量级：指数阶$O(2^n)$和阶乘阶$O(n!)$，当数据规模$n$越来越大时，非多项式量级算法的执行时间会急剧增加，求解问题的执行时间会无线增长。所以，非多项式时间复杂度的算法是非常低效的。

$O(1)$

$O(1)$只是常量级时间复杂度的一种表示方法，并不是指执行了一行代码。比如这段代码，即便有 3 行，它的时间复杂度也是$O(1）$，而不是$O(3)$。

1
2
3
int i = 8;
int j = 6;
int sum = i + j;

只要代码的执行时间不随$n$的增大而增长，这样代码的时间复杂度我们都记作$O(1)$。或者说，一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是$Ο(1)$。

$O(logn)$和$O(nlogn)$

对数阶时间复杂度非常常见，同时也是最难分析的一种时间复杂度。我通过一个例子来说明一下。

1
2
3
4
i=1;
while (i <= n)  {
	i = i * 2;
}

第三行代码是循环执行次数最多的。所以，我们只要能计算出这行代码被执行了多少次，就能知道整段代码的时间复杂度。

从代码中可以看出，变量 i 的值从 1 开始取，每循环一次就乘以 2。当大于 n 时，循环结束。实际上，变量 i 的取值就是一个等比数列。如果把它一个一个列出来，就应该是这个样子的：
01

所以，我们只要知道$x$值是多少，就知道这行代码执行的次数了。通过$2^x=n$求解$x={log_2}n$，所以，这段代码的时间复杂度就是$O({log_2}n)$。

现在，把代码稍微改下，你再看看，这段代码的时间复杂度是多少？

1
2
3
4
i=1;
while (i <= n)  {
	i = i * 3;
}

根据刚刚的思路，很简单就能看出来，这段代码的时间复杂度为$O({log_3}n)$。

实际上，不管是以 2 为底、以 3 为底，还是以 10 为底，我们可以把所有对数阶的时间复杂度都记为 $O(logn)$。为什么呢？

我们知道，对数之间是可以互相转换的，${log_3}n$ 就等于 ${log_3}2 * {log_2}n$，所以 $O({log_3}n) = O(C * {log_2}n)$，其中 $C={log_3}2$是一个常量。基于我们前面的一个理论：在采用大$O$ 标记复杂度的时候，可以忽略系数，即 $O(Cf(n)) = O(f(n))$。所以，$O({log_2}n) $就等于 $O({log_3}n)$。因此，在对数阶时间复杂度的表示方法里，忽略对数的“底”，统一表示为 $O(logn)$。

基于以上的$O(logn)$，那 $O(nlogn)$ 就很容易理解了。还记得乘法法则吗？如果一段代码的时间复杂度是 O(logn)，循环执行 $n$ 遍，时间复杂度就是 $O(nlogn)$ 了。而且，$O(nlogn)$也是一种非常常见的算法时间复杂度。比如，归并排序、快速排序的时间复杂度都是 $O(nlogn)$。

$O(m+n)$和$O(m*n)$

再来讲一种跟前面都不一样的时间复杂度，代码的复杂度由两个数据的规模来决定。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int cal(int m, int n) {
	int sum_1 = 0;
	int i = 1;
	for (; i < m; ++i) {
		sum_1 = sum_1 + i;
	}

	int sum_2 = 0;
	int j = 1;
	for (; j < n; ++j) {
		sum_2 = sum_2 + j;
	}

	return sum_1 + sum_2;
}

从代码中可以看出，m 和 n 是表示两个数据规模。我们无法事先评估 m 和 n 谁的量级大，所以我们在表示复杂度的时候，就不能简单地利用加法法则，省略掉其中一个。所以，上面代码的时间复杂度就是 $O(m+n)$。

针对这种情况，原来的加法法则就不正确了，需要将加法规则改为：$T1(m) + T2(n) = O(f(m) + g(n))$。但是乘法法则继续有效：$T1(m)*T2(n) = O(f(m) * f(n))$。

空间复杂度分析

理解了前面的大$O$表示法和时间复杂度分析，空间复杂度分析方法学起来就非常简单了。

时间复杂度的全称是渐进时间复杂度，表示算法的执行时间与数据规模之间的增长关系。类比一下，空间复杂度全称就是渐进空间复杂度，表示算法的存储空间与数据规模之间的增长关系。

1
2
3
4
5
6
7
8
9
10
11
void print(int n) {
	int i = 0;
	int[] a = new int[n];
	for (i; i <n; ++i) {
		a[i] = i * i;
	}

	for (i = n-1; i >= 0; --i) {
		print out a[i]
	}
}

跟时间复杂度分析一样，我们可以看到，第 2 行代码中，我们申请了一个空间存储变量 i，但是它是常量阶的，跟数据规模$n$没有关系，所以我们可以忽略。第 3 行申请了一个大小为$n$的 int 类型数组，除此之外，剩下的代码都没有占用更多的空间，所以整段代码的空间复杂度就是$O(n)$。

常见的空间复杂度就是 $O(1)$、$O(n)$、$O(n^2)$，像 $O(logn)$、$O(nlogn)$ 这样的对数阶复杂度平时都用不到。而且，空间复杂度分析比时间复杂度分析要简单很多。所以，对于空间复杂度，掌握这些内容已经足够了。